Table of Content
- Introduction
- Working of Support Vector Machine
- Support Vector Machines Kernels
- Advantages
- Disadvantages
- Support Vector Machine Use Cases
- Implementation
- Conclusion and Summary
Introduction
Support Vector Machine or SVM as it is briefly known was first introduced in the 1960's and with couple of iteration's later improvised in the 1990's. An SVM is a supervised machine learning algorithm used exclusively for classification or prediction. But the best used cases have been for classification rather than point predictions. There has been an increased adaption and popularization of this technique because of the ease of usage and high efficiency. SVM as compared to other machine learning algorithms possesses the capability of performing classification, regression, and outlier detection as well. A support vector machine is a discriminative classifier that is formally designed by a separate hyper-plane. The algorithm finds a linear hyperplane that separates the two classes using the maximum distance between the hyperplane and the nearest instance in each class.. In addition, an SVM can also perform non – linear classification. A support vector machine is a machine learning algorithm used for classification and regression. When we say its a supervised learning algorithm, we mean it learns from a series of examples with known labels, and then assigns labels to new data points.
Working of Support Vector Machine
The main objective of the Support Vector Machine is to segregate the given data in the best possible way. When the segregation is done, the distance between the nearest points is known as margin. The approach is to find a hyper-plane so as tp create the maximum possible margin between the support vectors in the given dataset. The support vector machine follows the following:
- It generates a hyper-plane that segregates the classes in the best possible ways.
- It selects the right hyper-plane with the maximum segregation from either nearest data points.
In some cases, while dealing with inseparable and non-linear plains the hyper-planes cannot be very efficient and in those cases, the SVM uses a kernel trick to transform the input into a higher dimensional space so with this it becomes easier to segregate the points.
Support Vector Machines Kernels
An SVM kernel is used to add more dimensions to a lower dimension space to make it easier to segregate the data. It converts the inseparable problems to a separable problem by adding more dimensions using the kernel trick. A Support Vector Machine is always implemented in practice by a kernel, the kernel trick helps to make it a more accurate classifier.
Different Types of the kernel in SVM are:
- Linear Kernels
- Polynomial Kernels
- Radial Basis Function Kernels
Linear Kernels
A linear kernel can be used as a normal dot product between any two given observations, the product between the vectors is the sum of the multiplication of each pair of input values.
Polynomial Kernels
A polynomial Kernel is a rather generalized form of the linear kernel, it can distinguish between curved and non-linear input phases.
Radial Basis Function Kernels (RBF)
The radial basis kernel of the RBF kernel is commonly used in SVM classification, it can map the space into infinite dimensions which is an advantage of the RBF kernel.
Advantages of SVM
- It is effective in high dimensional spaces
- It is still effective in cases where the no. of dimensions is greater than the no. of samples
- It uses a subset of training point in the decision function that makes it memory efficient
- Different kernel function can be specified for the decision function which also makes it versatile
Disadvantages of SVM
-
We may have a over fitting issue if the number of features or columns are larger that the samples or records.
-
Support Vector Machines do not directly provide probability estimate these are calculated using 5 fold cross-validation
Support Vector Machine Use Cases
- Face Detection
- Text and Hypertext Categorization
- Classification of Images
- Bioinformatics
- Remote Homology Detection
- Handwriting Detection
- Generalized Predictive Control
Implementation
Importing Libraries and Data
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import train_test_split
from sklearn.svm import SVR
# Download the data set used in this SVM case study by clicking here
house_df = pd.read_csv('house_sales_data.csv')
pd.set_option('display.max_columns', None)
house_df
id date price bedrooms bathrooms sqft_living sqft_lot floors waterfront view condition grade sqft_above sqft_basement yr_built yr_renovated zipcode lat long sqft_living15 sqft_lot15
0 7129300520 20141013T000000 221900.0 3 1.00 1180 5650 1.0 0 0 3 7 1180 0 1955 0 98178 47.5112 -122.257 1340 5650
1 6414100192 20141209T000000 538000.0 3 2.25 2570 7242 2.0 0 0 3 7 2170 400 1951 1991 98125 47.7210 -122.319 1690 7639
2 5631500400 20150225T000000 180000.0 2 1.00 770 10000 1.0 0 0 3 6 770 0 1933 0 98028 47.7379 -122.233 2720 8062
3 2487200875 20141209T000000 604000.0 4 3.00 1960 5000 1.0 0 0 5 7 1050 910 1965 0 98136 47.5208 -122.393 1360 5000
4 1954400510 20150218T000000 510000.0 3 2.00 1680 8080 1.0 0 0 3 8 1680 0 1987 0 98074 47.6168 -122.045 1800 7503
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
21608 263000018 20140521T000000 360000.0 3 2.50 1530 1131 3.0 0 0 3 8 1530 0 2009 0 98103 47.6993 -122.346 1530 1509
21609 6600060120 20150223T000000 400000.0 4 2.50 2310 5813 2.0 0 0 3 8 2310 0 2014 0 98146 47.5107 -122.362 1830 7200
21610 1523300141 20140623T000000 402101.0 2 0.75 1020 1350 2.0 0 0 3 7 1020 0 2009 0 98144 47.5944 -122.299 1020 2007
21611 291310100 20150116T000000 400000.0 3 2.50 1600 2388 2.0 0 0 3 8 1600 0 2004 0 98027 47.5345 -122.069 1410 1287
21612 1523300157 20141015T000000 325000.0 2 0.75 1020 1076 2.0 0 0 3 7 1020 0 2008 0 98144 47.5941 -122.299 1020 1357
Understanding the Data
house_df.isnull().sum()
id 0
date 0
price 0
bedrooms 0
bathrooms 0
sqft_living 0
sqft_lot 0
floors 0
waterfront 0
view 0
condition 0
grade 0
sqft_above 0
sqft_basement 0
yr_built 0
yr_renovated 0
zipcode 0
lat 0
long 0
sqft_living15 0
sqft_lot15 0
dtype: int64
We observe that there are no missing values in the data.
house_df.shape
(21613, 21)
So we have 21 columns and a total of 21,613 records. Next lets check the column names for functional understanding.
house_df.columns
Index(['id', 'date', 'price', 'bedrooms', 'bathrooms', 'sqft_living',
'sqft_lot', 'floors', 'waterfront', 'view', 'condition', 'grade',
'sqft_above', 'sqft_basement', 'yr_built', 'yr_renovated', 'zipcode',
'lat', 'long', 'sqft_living15', 'sqft_lot15'],
dtype='object')
We need to check the summary statistics of the data. We use the describe function to understand the distribution of data
house_df.describe()
id price ... sqft_living15 sqft_lot15
count 2.161300e+04 2.161300e+04 ... 21613.000000 21613.000000
mean 4.580302e+09 5.400881e+05 ... 1986.552492 12768.455652
std 2.876566e+09 3.671272e+05 ... 685.391304 27304.179631
min 1.000102e+06 7.500000e+04 ... 399.000000 651.000000
25% 2.123049e+09 3.219500e+05 ... 1490.000000 5100.000000
50% 3.904930e+09 4.500000e+05 ... 1840.000000 7620.000000
75% 7.308900e+09 6.450000e+05 ... 2360.000000 10083.000000
max 9.900000e+09 7.700000e+06 ... 6210.000000 871200.000000
A quick look at the data type.
house_df.info()
RangeIndex: 21613 entries, 0 to 21612
Data columns (total 21 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 id 21613 non-null int64
1 date 21613 non-null object
2 price 21613 non-null float64
3 bedrooms 21613 non-null int64
4 bathrooms 21613 non-null float64
5 sqft_living 21613 non-null int64
6 sqft_lot 21613 non-null int64
7 floors 21613 non-null float64
8 waterfront 21613 non-null int64
9 view 21613 non-null int64
10 condition 21613 non-null int64
11 grade 21613 non-null int64
12 sqft_above 21613 non-null int64
13 sqft_basement 21613 non-null int64
14 yr_built 21613 non-null int64
15 yr_renovated 21613 non-null int64
16 zipcode 21613 non-null int64
17 lat 21613 non-null float64
18 long 21613 non-null float64
19 sqft_living15 21613 non-null int64
20 sqft_lot15 21613 non-null int64
dtypes: float64(5), int64(15), object(1)
memory usage: 3.5+ MB
Data Pre-Processing
# dropping the date and id field as not required house_df.drop(['date', 'id'], axis = 1, inplace = True) plt.figure(figsize = (15,12)) sns.heatmap(house_df.corr(), annot = True, cmap = 'magma') plt.show()
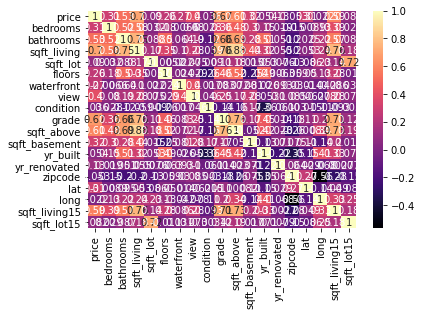
Figure 1 : House price data correlation plot
# dropping columns which dont have corelation an relevancy house_df = house_df.drop(['condition', 'zipcode', 'long', 'sqft_lot15', 'waterfront', 'view', 'sqft_basement', 'yr_renovated'], axis = 1) house_df price bedrooms bathrooms ... yr_built lat sqft_living15 0 221900.0 3 1.00 ... 1955 47.5112 1340 1 538000.0 3 2.25 ... 1951 47.7210 1690 2 180000.0 2 1.00 ... 1933 47.7379 2720 3 604000.0 4 3.00 ... 1965 47.5208 1360 4 510000.0 3 2.00 ... 1987 47.6168 1800 ... ... ... ... ... ... ... 21608 360000.0 3 2.50 ... 2009 47.6993 1530 21609 400000.0 4 2.50 ... 2014 47.5107 1830 21610 402101.0 2 0.75 ... 2009 47.5944 1020 21611 400000.0 3 2.50 ... 2004 47.5345 1410 21612 325000.0 2 0.75 ... 2008 47.5941 1020 [21613 rows x 11 columns]
Splitting data
X = house_df.drop(['price'], axis = 1)
Y = house_df['price']
Training Model
scaler = MinMaxScaler(feature_range=(0, 1))
scaler.fit(X)
X_Scaler = scaler.transform(X)
X_train, X_test, Y_train, Y_test = train_test_split(X_Scaler, Y, test_size = 0.2, random_state = 2)
model = SVR(kernel = 'linear')
model.fit(X_train, Y_train)
Model Evaluation
model.score(X_test, Y_test)
predictions = model.predict(X_test)
predictions
array([450367.72306356, 450524.68977382, 450087.47563024, ...,
450193.8994151 , 449453.92018701, 449700.14385532])
Prediction Using New Manual fed Data
X_new = [[2, 0.75, 1020, 1350, 2.0, 7, 1020, 2009, 47.5944, 1020]]
X_newScaler = scaler.transform(X_new)
float(model.predict(X_newScaler))
450128.90560640447
Conclusion and Summary
In this tutorial, we discussed the Support Vector Machine (SVM) and using it for regression. Also, we discussed the working of a support machine, various kernels, advantages, disadvantages, and various use cases of an SVM , further on, we also built a model for predicting the house prices using various independent variables. You can check out this quick implementation of Support Vector Machines for Hand Written Alphabet Recognition.
About the Author's:

Write A Public Review